from datascience import *
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import plotly.express as px
Table.interactive_plots()
Note: We're not going to be able to work through this entire notebook in lecture; you should definitely review whatever we don't get a chance to finish.
World University Rankings 2020¶
Our dataset comes from Times Higher Education (THE)'s World University Rankings 2020. These are slightly outdated as there is a 2021 ranking now, but the data is still relevant.
world = Table.read_table('data/World_University_Rank_2020.csv')
world
It's always good to check how many schools we're dealing with:
world.num_rows
Some columns ('Number_students', 'International_Students', 'Percentage_Female', 'Percentage_Male') have commas and percentage symbols, meaning they can't be stored as integers. Let's clean them.
# Notice how we use apply here!
def remove_symbol(s):
return int(s.replace('%', '').replace(',', ''))
# Remember, the result of calling apply is an array
world.apply(remove_symbol, 'Number_students')
world = world.with_columns(
'Number_students', world.apply(remove_symbol, 'Number_students'),
'International_Students', world.apply(remove_symbol, 'International_Students'),
'Percentage_Female', world.apply(remove_symbol, 'Percentage_Female'),
'Percentage_Male', world.apply(remove_symbol, 'Percentage_Male')
)
Now we can sort by any numeric column we want.
world.sort('Percentage_Female')
It seems like the above schools didn't report their sex breakdown, since 0% is the listed percentage of female and male students.
Let's start asking questions.
Which universities have the most international students?¶
We have an 'International_Students' column, but that tells us the percentage of international students at each school. Let's update that label to be more clear – let's change the label 'International_Students' to be '% International'.
world = world.relabeled('International_Students', '% International')
world
Then, to compute the number of international students at each school, we take the number of students at each school, multiply by the percentage of international students at each school, and divide by 100.
world.column('Number_students') * world.column('% International') / 100
We should probably round the result, since we can't have fractional humans.
num_international = np.round(world.column('Number_students') * world.column('% International') / 100, 0)
num_international
We can add this as a column to our table:
world = world.with_columns(
'# International', num_international
)
And we can sort by this column, while also selecting a subset of all columns just to focus on what's relevant:
world.select('University', 'Country', 'Number_students', '% International', '# International') \
.sort('# International', descending = True)
This tells us that the University of Melbourne has the most international students, with 21,797. That's larger than many universities!
There are no US universities in the top 10 here. How can we find the universities in the US with the most international students?
Quick Check 1¶
Fill in the blanks so that the resulting table contains the 15 universities in the US with the most international students, sorted by number of international students in decreasing order.
# __(a)__ means blank a
# world.select('University', 'Country', 'Number_students', '% International', '# International') \
# .where(__(a)__, __(b)__) \
# .sort('# International', __(c)__) \
# .take(__(d)__)
If you do a quick Google search for "US universities with the most international students", you'll see NYU is usually #1. Cool!
How do the rankings actually work?¶
Times Higher Education's website tells us the methodology they use to rank universities:
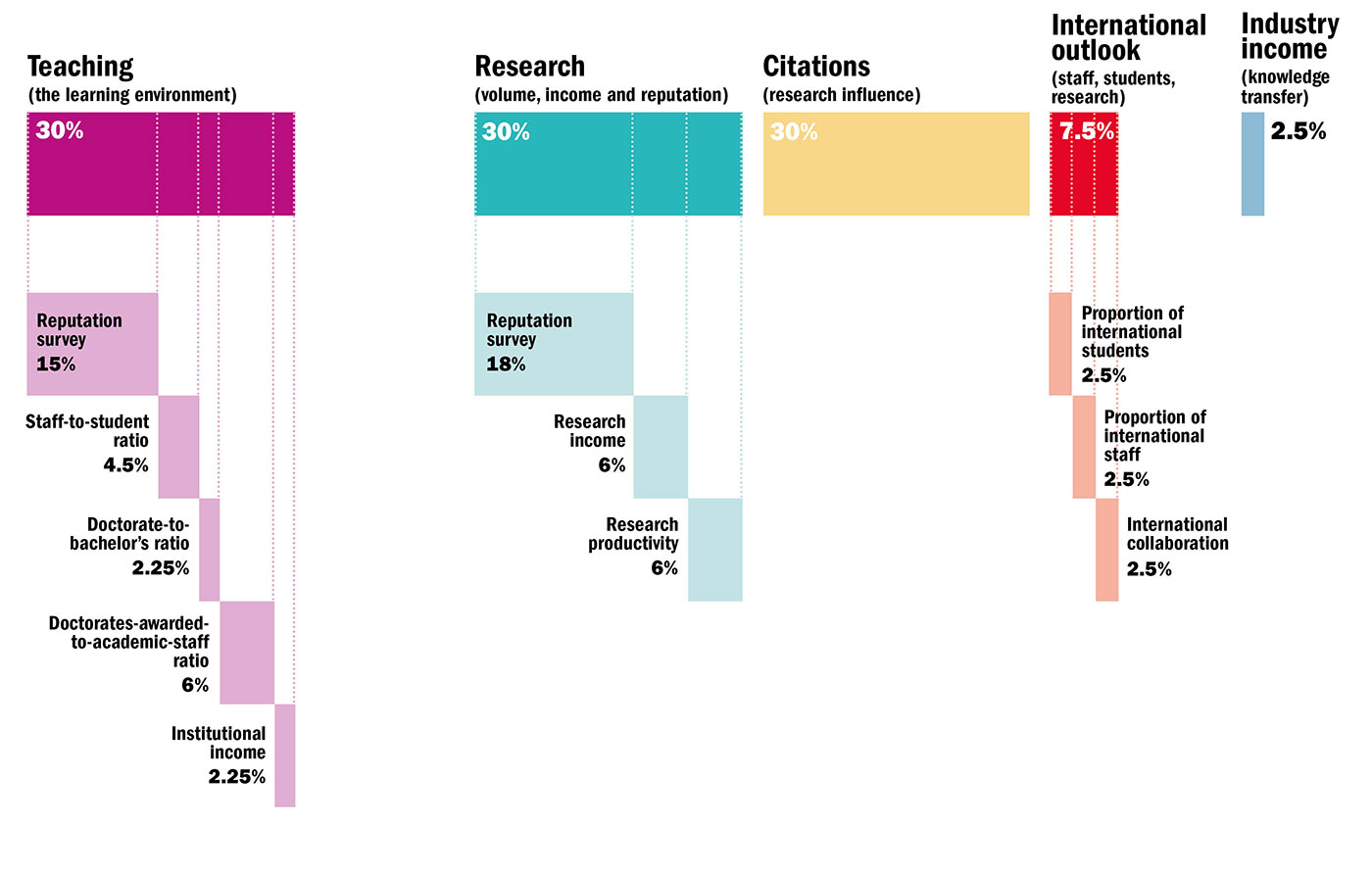
This means they come up with a 'Teaching', 'Research', 'Citations', 'International_Outlook', and 'Industry_Income' score from 0 to 100 for each school, then compute a weighted average according to the above percentages to compute a school's 'Score_Result', which is how the schools are ranked.
Let's confirm this ourselves. First, let's get a subset of the columns since they won't all be relevant here.
scores_only = world.select('Score_Rank', 'University', 'Teaching', 'Research', 'Citations', 'International_Outlook', 'Industry_Income', 'Score_Result')
scores_only
The graphic tells us that the weights for each column are:
'Teaching': 0.3'Research': 0.3'Citations': 0.3'International_Outlook': 0.075'Industry_Income': 0.025
(Remember, to convert from percentage to proportion we divide by 100.)
Let's try and apply this to the school at the very top of the table, University of Oxford.
0.3 * 90.5 + \
0.3 * 99.6 + \
0.3 * 98.4 + \
0.075 * 96.4 + \
0.025 * 65.5
The result, 95.4175, matches what we see in the 'Score_Result' column for University of Oxford.
We can apply the above formula to all rows in our table as well.
score_result_manual_calculation = \
0.3 * scores_only.column('Teaching') + \
0.3 * scores_only.column('Research') + \
0.3 * scores_only.column('Citations') + \
0.075 * scores_only.column('International_Outlook') + \
0.025 * scores_only.column('Industry_Income')
score_result_manual_calculation
To confirm that the results we got match the 'Score_Result' column in scores_only, we can add the above array to our table:
scores_only.with_columns(
'Score Result Manual', score_result_manual_calculation
)
This shows we've successfully reverse-engineered how the rankings work!
What if we want to change the methodology?¶
Now that we know how to compute 'Score_Result's using THE's percentages, we can also pick our own percentages if we want to prioritize different components in our ranking.
For instance, we may feel like THE's methodology places too much emphasis on research – together, 'Research' and 'Citations' make up 60% of the overall score.
We could choose to use the following breakdown, which we'll call "Breakdown 1":
'Teaching': 60%'International_Outlook': 30%'Industry_Income': 10%
breakdown_1 = 0.6 * scores_only.column('Teaching') \
+ 0.3 * scores_only.column('International_Outlook') \
+ 0.1 * scores_only.column('Industry_Income')
breakdown_1
This gives us new overall scores for each school; we can add this column to our table and sort by it.
scores_only = scores_only.with_columns(
'Breakdown 1', breakdown_1
)
scores_only.sort('Breakdown 1', descending = True)
scores_only.sort('Breakdown 1', descending = True).take(23)
Note that when we choose this methodology, UC Berkeley is ranked much lower (24th instead of 13th). This is likely due to:
- UC Berkeley's exceptionally high
'Research'and'Citations'scores not being included in the ranking
- UC Berkeley's exceptionally high
- UC Berkeley's large class sizes giving it a comparatively low
'Teaching'score
- UC Berkeley's large class sizes giving it a comparatively low
- UC Berkeley's low score for
'Industry_Income'. This component factors in the amount that the university receives in funding from industrial partners – given that it's a public school it's unsurprising that this amount is low, but also many "wealthy" universities have a relatively low score here too, so it's not clear how much this should matter (see here for more).
- UC Berkeley's low score for
Maybe we want to place some emphasis on research, but not as much as was placed in the initial ranking. We could then make "Breakdown 2":
'Teaching': 50%'Research': 15%'Citations': 15%'International_Outlook': 15%'Industry_Income': 5%
Quick Check 2¶
Assign breakdown_2 to an array of overall scores for schools calculated according to our Breakdown 2 above, and add it as a column to scores_only with the label 'Breakdown 2'. _Hint: Start by copying our code for breakdown_1, which was:_
breakdown_1 = 0.6 * scores_only.column('Teaching') \
+ 0.3 * scores_only.column('International_Outlook') \
+ 0.1 * scores_only.column('Industry_Income')
# Answer QC here before running the next cell
scores_only.sort('Breakdown 2', descending = True)
"Breakdown 2" is much closer to THE's actual breakdown and the ordering here reflects that.
What do you care about in a university? Try your own breakdown!
We should note though that we haven't really thought about how THE comes up with the scores for each of the five categories (or the fact that university rankings have inherent flaws).
Which countries have the most universities in the ranking?¶
Back to the full world table:
world
To determine the number of universities per country, we can group by 'Country':
world.group('Country')
It's a good idea to sort too:
world.group('Country').sort('count', descending = True)
How do we get the number of universities in each country with at least 25 universities on the list?
world.group('Country').where('count', are.above_or_equal_to(25))
Run the cell below to see a bar graph of the number of universities in each country above.
world.group('Country').where('count', are.above_or_equal_to(25)).sort('count').barh('Country')
No surprises here!
We could also determine the average 'Score_Rating' for every country in the list.
world.group('Country', np.mean)
We need to select the relevant columns here and then sort.
world.group('Country', np.mean).select('Country', 'Score_Result mean').sort('Score_Result mean', descending = True)
This tells us which countries have the "best" universities according to ranking. However, many of the countries at the top are small:
world.where('Country', 'Singapore')
There are only two universities on the list from Singapore, and they're both ranked relatively high.
What's the best university in each country?¶
It turns out this can be answered by grouping with a particular collect function.
def first(arr):
return arr.item(0)
When we group by 'Country' and use first as our collectfunction, we get the first row for each country in the table. Since the world table is sorted by ranking to begin with, we don't need to sort before grouping.
world.group('Country', first)
Let's sort the resulting table by ranking (and also extract a few relevant columns):
world.group('Country', first) \
.sort('Score_Result first', descending = True) \
.select('Score_Rank first', 'Country', 'University first', 'Score_Result first')
By default, the column we grouped by (so 'Country') is the left-most column, but because we selected them in a different order in the last line above they appear in a different order.
What the 'Score_Rank first' column tells us is how highly-ranked the best university in each country is. It tells us the best university in Canada is 17th best in the world, and the best university in Japan is 33rd best in the world – again, according to THE.
Question: What if we wanted the second best, or third best, university in each country?
In which states are the best US universities located?¶
So far we've been looking at universities across the world. We may want to zoom in on just universities in the US (and also select just a few relevant columns):
us_only = world.where('Country', 'United States') \
.select('University', 'Number_students', 'Score_Result')
us_only
Right now we don't have any information about where these schools are located within the US.
But we can get that information! Let's refer to Wikipedia's article List of research universities in the United States for help. There are two tables there: one for "R1: Doctoral Universities – Very high research activity" and one for "R2: Doctoral Universities – High research activity". For simplicity's sake we'll take just the first table, since the majority of schools in us_only will be contained in it.
Run the cell below to load that table in.
If you're curious as to how we downloaded the information from Wikipedia: We used this site, which allows you to specify a Wikipedia URL and gives you a CSV file.
us_r1 = Table.read_table('data/us-r1-universities.csv')
us_r1
Now, let's join the two tables together. We want to look for matches between the 'University' column in us_only and the 'Institution' column in us_r1.
# Think about why these are the arguments to join!
us_with_state = us_only.join('University', us_r1, 'Institution')
us_with_state
The above table only has 96 rows, whereas the bar chart earlier told us there were 172 US schools in our rankings table. That likely means we lost rows as a result of:
- School names not matching between the two tables (maybe one column had a typo or alternative name)
- School names not being in
us_r1
At a glance though it doesn't seem like there are major omissions, since all of the top 10 US schools are still there:
us_with_state.sort('Score_Result', descending = True)
Let's proceed. Since our original goal was to determine the states in which the best schools were, we can group by 'State' – first with no aggregation function, and then with np.mean to look at the average 'Score_Result' for each state.
us_with_state.group('State').sort('count', descending = True)
# sort(1) means sort by the column at index 1, which is 'Score_Result mean'
us_with_state.group('State', np.mean).select('State', 'Score_Result mean').sort(1, descending = True)
The above tells us that California had the most high-ranked schools in the dataset, while Maryland has the highest average ranking amongst all states in the dataset. However, just like with Singapore earlier, there aren't many schools from Maryland:
us_with_state.where('State', 'MD')
Followup – how do public and private schools in the US compare?¶
The us_r1 table brought us more information that we haven't yet used – it gave us information about whether each school is public or private! Let's do some initial queries.
us_with_state.group('Control')
us_with_state.group('Control', np.mean)
It seems like there are fewer US private schools in the dataset, but they're ranked higher than the public schools in the dataset on average. They're also smaller on average, at ~16,000 to ~31,000.
Since we have two categories, we can group:
us_with_state.group(['State', 'Control'])
But an easier way to look at the above would be to create a pivot table:
us_with_state.pivot('Control', 'State')
If we want the states with the most public schools in the ranking:
us_with_state.pivot('Control', 'State').sort('Public', descending = True)
What if we want the average 'Score_Result' for each state, separated by public vs. private? We can do that too.
us_with_state.pivot('Control', 'State', 'Score_Result', np.mean)
This, in theory, gives us the states with the "best" public universities at the top.
us_with_state.pivot('Control', 'State', 'Score_Result', np.mean).sort('Public', descending = True)
This doesn't mean a whole lot, since the number of public universities in each state is wildly different.
For example, we see Minnesota ('MN') is the second row – there's only one school in the dataset from Minnesota!
us_with_state.where('State', 'MN')
A warning¶
If you pivot with columns that don't really make sense, you'll get weird results:
us_with_state.pivot('State', 'University')
Done!¶
Make sure to review all of the code in this notebook, as it's all great review for the quiz.